출처 : Wikipedia
A weight function is a mathematical device used when performing a sum, integral, or average in order to give some elements more of a "weight" than others. They occur frequently in statistics and analysis, and are closely related to the concept of a measure. Weight functions can be constructed in both discrete and continuous settings.
Continuous weights
In the continuous setting, a weight is a positive measure such as w(x)dx on some domain Ω,which is typically a subset of an Euclidean space

, for instance Ω could be an interval[a,b]. Here dx is Lebesgue measure and
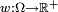
is a non-negative measurablefunction. In this context, the weight function w(x) is sometimes referred to as a density.
General definition
If

is a real-valued function, then the unweighted integral
can be generalized to the >weighted integral
Note that one may need to require f to be absolutely integrable with respect to the weight w(x)dx in order for this integral to be finite.
Weighted volume
If E is a subset of Ω, then the volume vol(E) of E can be generalized to the weighted volume
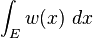
.
Weighted average
If Ω has finite non-zero weighted volume, then we can replace the unweighted average $ \frac{1}{\text{vol} \left( \Omega \right)}\int_{\Omega}^{}f\left( x \right)dx $ by the weighted average $\frac{\int_{\Omega}^{}f\left( x \right)w\left( x \right)dx}{\int_{\Omega}^{}w\left( x \right)dx}$
Inner product
If $f:\Omega\to \mathbb{R} $ and $g:\Omega\to \mathbb{R} $ are two functions, one can generalize the unweighted inner product $\left\langle f,g \right\rangle :=\int_{\Omega}^{}f\left( x \right)g\left( x \right)dx$ to a weighted inner product $\left\langle f,g \right\rangle :=\int_{\Omega}^{}f\left( x \right)g\left( x \right)w\left( x \right)dx$
'Major > Math' 카테고리의 다른 글
| Vector Identity (0) | 2025.01.01 |
|---|---|
| 사인법칙 (Law of sines), 코사인법칙 (Law of cosines) (0) | 2023.03.13 |
| 삼각함수 공식 (Trigonometric Relations) (0) | 2022.07.18 |
| Integral Asymptotics- Stationary Phase Method (0) | 2021.10.17 |
| 테일러 급수 (Taylor Series) (0) | 2017.11.03 |




댓글